Optimal Control of a Rocket¶

This example is adapted from the JuMP tutorial.

The goal is to show that there are explicit repeated structures in discretized optimal control problem regarded as a nonlinear program (NLP). We will use the optimal control of a rocket as an example to demonstrate how to exploit these structures to solve the problem more efficiently via PyOptInterface.

Problem Formulation¶

The problem is to find the optimal control of a rocket to maximize the altitude at the final time while satisfying the dynamics of the rocket. The dynamics of the rocket are described by the following ordinary differential equations (ODEs):

\[\begin{split} \begin{align*} \frac{dh}{dt} &= v \\ \frac{dv}{dt} &= -g(h) + \frac{u-D(h,v)}{m} \\ \frac{dm}{dt} &= -\frac{u}{c} \end{align*} \end{split}\]

where \(h\) is the altitude, \(v\) is the velocity, \(m\) is the mass, \(u\) is the thrust, \(g(h)\) is the gravitational acceleration, and \(D(h,v)\) is the drag force. The thrust \(u\) is the control variable.

The drag force is given by \(D(h,v) = D_c v^2 \exp(-h_c \frac{h-h_0}{h_0})\), and the gravitational acceleration is given by \(g(h) = g_0 (\frac{h_0}{h})^2\).

By discretizing the ODEs, we obtain the following nonlinear program:

\[\begin{split} \begin{align*} \frac{h_{t+1}-h_t}{\Delta t} &= v_t \\ \frac{v_{t+1}-v_t}{\Delta t} &= -g(h_t) + \frac{u_t-D(h_t,v_t)}{m_t} \\ \frac{m_{t+1}-m_t}{\Delta t} &= -\frac{u_t}{c} \end{align*} \end{split}\]

where \(h_t\), \(v_t\), and \(m_t\) are the altitude, velocity, and mass at time \(t\), respectively, and \(\Delta t\) is the time step.

Implementation¶

In the discretized optimal control problem, the variables at two adjacent time points share the same algebraic relationship.

from math import sqrt
import pyoptinterface as poi
from pyoptinterface import nlfunc, ipopt

model = ipopt.Model()

h_0 = 1                      # Initial height
v_0 = 0                      # Initial velocity
m_0 = 1.0                    # Initial mass
m_T = 0.6                    # Final mass
g_0 = 1                      # Gravity at the surface
h_c = 500                    # Used for drag
c = 0.5 * sqrt(g_0 * h_0)    # Thrust-to-fuel mass
D_c = 0.5 * 620 * m_0 / g_0  # Drag scaling
u_t_max = 3.5 * g_0 * m_0    # Maximum thrust
T_max = 0.2                  # Number of seconds
T = 1_000                    # Number of time steps
delta_t = 0.2 / T;           # Time per discretized step

def rocket_dynamics(vars, params):
    m2, m1 = vars.m2, vars.m1
    h2, h1 = vars.h2, vars.h1
    v2, v1 = vars.v2, vars.v1
    u = vars.u

    h_eq = (h2 - h1) - delta_t * v1
    v_eq = (v2 - v1) - delta_t * (-g_0 * (h_0 / h1)**2 + (u - D_c * v1**2 * nlfunc.exp(-h_c * (h1 - h_0) / h_0)) / m1)
    m_eq = (m2 - m1) - delta_t * (-u / c)

    return [h_eq, v_eq, m_eq]

rd = model.register_function(rocket_dynamics)

Then, we declare variables and set boundary conditions.

v = model.add_variables(range(T), name="v", lb=0.0, start=v_0)
h = model.add_variables(range(T), name="h", lb=0.0, start=h_0)
m = model.add_variables(range(T), name="m", lb=m_T, ub=m_0, start=m_0)
u = model.add_variables(range(T), name="u", lb=0.0, ub=u_t_max, start=0.0)

model.set_variable_bounds(v[0], v_0, v_0)
model.set_variable_bounds(h[0], h_0, h_0)
model.set_variable_bounds(m[0], m_0, m_0)
model.set_variable_bounds(u[T-1], 0.0, 0.0)

Next, we add the dynamics constraints.

for t in range(T-1):
    model.add_nl_constraint(
        rd,
        vars=nlfunc.Vars(h2=h[t+1], h1=h[t], v2=v[t+1], v1=v[t], m2=m[t+1], m1=m[t], u=u[t]),
        eq=0.0,
    )

Finally, we add the objective function. We want to maximize the altitude at the final time, so we set the objective function to be the negative of the altitude at the final time.

model.set_objective(-h[T-1])

After solving the problem, we can plot the results.

model.optimize()

******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
 Ipopt is released as open source code under the Eclipse Public License (EPL).
         For more information visit http://projects.coin-or.org/Ipopt

This version of Ipopt was compiled from source code available at
    https://github.com/IDAES/Ipopt as part of the Institute for the Design of
    Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
    Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.

This version of Ipopt was compiled using HSL, a collection of Fortran codes
    for large-scale scientific computation.  All technical papers, sales and
    publicity material resulting from use of the HSL codes within IPOPT must
    contain the following acknowledgement:
        HSL, a collection of Fortran codes for large-scale scientific
        computation. See http://www.hsl.rl.ac.uk.
******************************************************************************

This is Ipopt version 3.13.2, running with linear solver ma27.

Number of nonzeros in equality constraint Jacobian...:    10983
Number of nonzeros in inequality constraint Jacobian.:        0
Number of nonzeros in Lagrangian Hessian.............:     7985

Total number of variables............................:     3996
                     variables with only lower bounds:     1998
                variables with lower and upper bounds:     1998
                     variables with only upper bounds:        0
Total number of equality constraints.................:     2997
Total number of inequality constraints...............:        0
        inequality constraints with only lower bounds:        0
   inequality constraints with lower and upper bounds:        0
        inequality constraints with only upper bounds:        0

iter    objective    inf_pr   inf_du lg(mu)  ||d||  lg(rg) alpha_du alpha_pr  ls
   0 -1.0000000e+00 1.02e-02 2.00e+00  -1.0 0.00e+00    -  0.00e+00 0.00e+00   0
   1 -9.9900008e-01 9.32e-03 1.82e+00  -1.0 1.89e-01    -  1.00e-01 8.60e-02f  1
   2 -9.9899675e-01 9.30e-03 9.71e+01  -1.0 4.00e+00    -  3.81e-02 1.83e-03f  1
   3 -1.0023330e+00 1.74e-04 2.26e+04  -1.0 1.49e+00    -  7.43e-02 9.81e-01f  1
   4 -1.0038323e+00 4.66e-05 6.03e+03  -1.0 2.14e+00    -  7.36e-01 7.33e-01f  1
   5 -1.0053212e+00 2.04e-06 3.51e+02  -1.0 3.82e-01    -  1.80e-01 1.00e+00f  1
   6 -1.0062108e+00 1.43e-06 3.11e+01  -1.0 2.77e-01    -  5.64e-01 1.00e+00f  1
   7 -1.0067054e+00 2.36e-06 1.38e+00  -1.0 2.99e-01    -  1.00e+00 1.00e+00f  1
   8 -1.0067009e+00 4.96e-10 5.89e-02  -2.5 3.58e-02    -  1.00e+00 1.00e+00h  1
   9 -1.0065674e+00 3.08e-07 1.40e-03  -2.5 8.48e-01    -  1.00e+00 1.00e+00f  1
iter    objective    inf_pr   inf_du lg(mu)  ||d||  lg(rg) alpha_du alpha_pr  ls
  10 -1.0065717e+00 1.85e-11 1.10e-03  -3.8 8.93e-04    -  1.00e+00 1.00e+00h  1
  11 -1.0066639e+00 7.76e-09 2.45e-03  -5.7 2.00e-02    -  9.93e-01 1.00e+00h  1
  12 -1.0105346e+00 2.22e-05 1.20e-03  -5.7 8.59e-01    -  1.00e+00 9.79e-01f  1
  13 -1.0106556e+00 3.08e-07 2.30e-05  -5.7 3.62e-01    -  1.00e+00 1.00e+00f  1
  14 -1.0106567e+00 1.16e-08 1.08e-07  -5.7 1.18e-01    -  1.00e+00 1.00e+00h  1
  15 -1.0122821e+00 1.07e-05 9.12e-04  -8.6 4.88e-01    -  7.71e-01 1.00e+00h  1
  16 -1.0126834e+00 7.79e-06 2.40e-04  -8.6 9.41e-01    -  7.31e-01 7.77e-01h  1
  17 -1.0127609e+00 3.53e-06 7.30e-05  -8.6 1.16e+00    -  6.90e-01 7.35e-01h  1
  18 -1.0127670e+00 2.61e-06 1.32e-04  -8.6 9.91e-01    -  7.65e-01 2.74e-01h  1
  19 -1.0127794e+00 3.72e-07 5.70e-04  -8.6 3.55e-01    -  8.94e-01 1.00e+00f  1
iter    objective    inf_pr   inf_du lg(mu)  ||d||  lg(rg) alpha_du alpha_pr  ls
  20 -1.0127794e+00 7.49e-08 4.51e-05  -8.6 2.25e-01    -  1.00e+00 8.85e-01h  1
  21 -1.0127794e+00 3.92e-08 6.47e-05  -8.6 1.12e-01    -  1.00e+00 5.00e-01f  2
  22 -1.0127794e+00 2.33e-09 4.28e-08  -8.6 5.82e-02    -  1.00e+00 1.00e+00h  1
  23 -1.0127794e+00 2.55e-13 4.12e-12  -8.6 1.01e-03    -  1.00e+00 1.00e+00h  1

Number of Iterations....: 23

                                   (scaled)                 (unscaled)
Objective...............:  -1.0127793922163879e+00   -1.0127793922163879e+00
Dual infeasibility......:   4.1223226930173622e-12    4.1223226930173622e-12
Constraint violation....:   2.5533313527739687e-13    2.5533313527739687e-13
Complementarity.........:   2.5059421407651927e-09    2.5059421407651927e-09
Overall NLP error.......:   2.5059421407651927e-09    2.5059421407651927e-09


Number of objective function evaluations             = 25
Number of objective gradient evaluations             = 24
Number of equality constraint evaluations            = 25
Number of inequality constraint evaluations          = 0
Number of equality constraint Jacobian evaluations   = 24
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations             = 23
Total CPU secs in IPOPT (w/o function evaluations)   =      0.125
Total CPU secs in NLP function evaluations           =      0.004

EXIT: Optimal Solution Found.

h_value = []
for i in range(T):
    h_value.append(model.get_value(h[i]))

print("Optimal altitude: ", h_value[-1])

Optimal altitude:  1.012779392216388

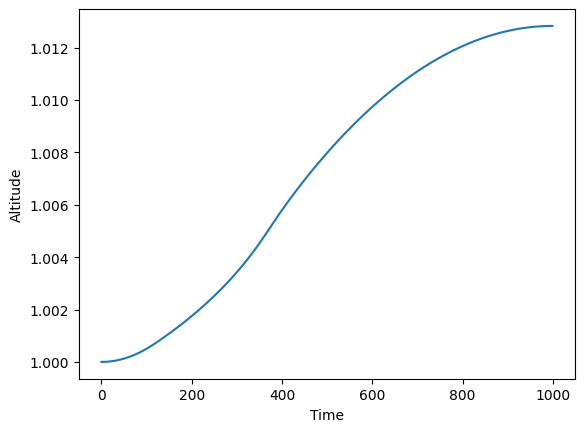
The plot of the altitude of the rocket is shown below.

import matplotlib.pyplot as plt

plt.plot(h_value)
plt.xlabel("Time")
plt.ylabel("Altitude")
plt.show()

../_images/ed1c7aea46382559ec32770aba1e641df510d8db1c0825be0e0078c61695ac09.png